Tail Recursion Optimization in Hotspot

Recursion can be more expensive than iterating over the same code.

Take this iterative method:


    int iterativeCall(int count, int maxCalls) {
        for (int i = 0 ; i < maxCalls ; i++) {
            count ^= count +1;
        }
        return count;
    }

And this recursive method:

    int recursiveCall(int count, int countDown) {
        if (countDown <= 0)
            return count;
        count ^= count +1;
        return recursiveCall(count, countDown - 1);
    }


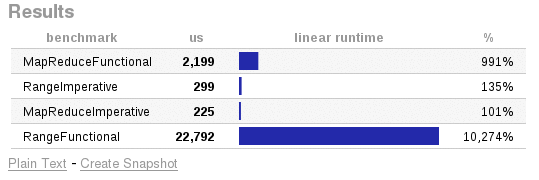
And compare the two. Using Caliper, the difference looks something like this:

To make recursive loops perform more like iterative loops, various tricks can be employed to make the compiled code loop over a block rather than jump recursively.

I noticed Hotspot do something similar to this. It's not fully optimized because it appears to reduce rather than avoid recursions.

This is how I did it. If we now add a static main method to our class containing the code above:


    public static void main(String[] args) {
        RecursionVsIterativeBenchmark app = new RecursionVsIterativeBenchmark();
        for (int i = 0 ; i < 1000 ; i++) {
            app.recursiveCall(0, 1000);
        }
    }


and run the code with:


/usr/java/jdk1.7.0.fastdebug/bin/java -XX:+UnlockDiagnosticVMOptions -XX:CompileCommand=print,com.henryp.test.recursion.RecursionVsIterativeBenchmark -server -XX:+PrintAssembly -XX:CompileThreshold=90000 -cp  /home/henryp/workspace/myPerformance/target/classes/:/home/henryp/.m2/repository/com/google/caliper/caliper/0.5-rc1/caliper-0.5-rc1.jar:/home/henryp/.m2/repository/com/google/code/findbugs/jsr305/1.3.9/jsr305-1.3.9.jar:/home/henryp/.m2/repository/com/google/code/gson/gson/1.7.1/gson-1.7.1.jar:/home/henryp/.m2/repository/com/google/guava/guava/11.0.1/guava-11.0.1.jar:/home/henryp/.m2/repository/com/google/code/java-allocation-instrumenter/java-allocation-instrumenter/2.0/java-allocation-instrumenter-2.0.jar:/home/henryp/.m2/repository/asm/asm/3.3.1/asm-3.3.1.jar:/home/henryp/.m2/repository/asm/asm-analysis/3.3.1/asm-analysis-3.3.1.jar:/home/henryp/.m2/repository/asm/asm-commons/3.3.1/asm-commons-3.3.1.jar:/home/henryp/.m2/repository/asm/asm-tree/3.3.1/asm-tree-3.3.1.jar:/home/henryp/.m2/repository/asm/asm-util/3.3.1/asm-util-3.3.1.jar:/home/henryp/.m2/repository/asm/asm-xml/3.3.1/asm-xml-3.3.1.jar com.henryp.test.recursion.RecursionVsIterativeBenchmark

to make hotspot spit out the assembly code, we see:


{method} 
 - klass: {other class}
 - this oop:          0x000000040d0e7970
 - method holder:     'com/henryp/test/recursion/RecursionVsIterativeBenchmark'
 - constants:         0x000000040d0e7078 constant pool [42] for 'com/henryp/test/recursion/RecursionVsIterativeBenchmark' cache=0x000000040d1372c0
 - access:            0x81000000  
 - name:              'recursiveCall'
 - signature:         '(II)I'
 - max stack:         4
 - max locals:        3
 - size of params:    3
 - method size:       17
 - vtable index:      21
 - i2i entry:         0x00007f8d0501d960
 - adapter:           0x00007f8d080b8f20
 - compiled entry     0x00007f8d050dc877
 - code size:         21
 - code start:        0x000000040d0e7928
 - code end (excl):   0x000000040d0e793d
 - method data:       0x000000040d193b08
 - checked ex length: 0
 - linenumber start:  0x000000040d0e793d
 - localvar length:   3
 - localvar start:    0x000000040d0e794a
#
#  int ( com/henryp/test/recursion/RecursionVsIterativeBenchmark:NotNull *, int, int )
#
#r018 rsi:rsi   : parm 0: com/henryp/test/recursion/RecursionVsIterativeBenchmark:NotNull *
#r016 rdx   : parm 1: int
#r010 rcx   : parm 2: int
# -- Old rsp -- Framesize: 32 --
#r089 rsp+28: pad2, in_preserve
#r088 rsp+24: pad2, in_preserve
#r087 rsp+20: pad2, in_preserve
#r086 rsp+16: pad2, in_preserve
#r085 rsp+12: pad2, in_preserve
#r084 rsp+ 8: return address
#r083 rsp+ 4: Fixed slot 1
#r082 rsp+ 0: Fixed slot 0
#
000   N94: # B1 <- 1="" block="" font="" freq:="" head="" is="" junk="" nbsp="">
000   movl    rscratch1, [j_rarg0 + oopDesc::klass_offset_in_bytes()] # compressed klass
decode_heap_oop_not_null rscratch1, rscratch1
cmpq    rax, rscratch1 # Inline cache check
jne     SharedRuntime::_ic_miss_stub
nop # nops to align entry point

      nop # 12 bytes pad for loops and calls

020   B1: # B6 B2 <- 1="" block="" font="" freq:="" head="" is="" junk="" nbsp="">
020   # stack bang
pushq   rbp
subq    rsp, #16 # Create frame
02c   testl   RCX, RCX
02e   jle,s   B6  P=0.001002 C=198529.000000
02e
030   B2: # B7 B3 <- 0.998998="" b1="" font="" nbsp="" req:="">
030   movl    R11, RCX # spill
033   decl    R11 # int
036   movl    R8, RDX # spill
039   incl    R8 # int
03c   xorl    R8, RDX # int
03f   testl   R11, R11
042   jle,s   B7  P=0.001002 C=198529.000000
042
044   B3: # B5 B4 <- 0.997996="" b2="" font="" nbsp="" req:="">
044   movl    R11, RCX # spill
047   addl    R11, #-2 # int
04b   movl    RAX, R8 # spill
04e   incl    RAX # int
050   xorl    RAX, R8 # int
053   testl   R11, R11
056   jle,s   B5  P=0.001002 C=198529.000000
056
058   B4: # B8 B5 <- 0.996996="" b3="" font="" nbsp="" req:="">
058   addl    RCX, #-3 # int
05b   movl    RDX, RAX # spill
05d   incl    RDX # int
05f   xorl    RDX, RAX # int
061   nop # 2 bytes pad for loops and calls
063   call,static  com.henryp.test.recursion.RecursionVsIterativeBenchmark::recursiveCall
        # com.henryp.test.recursion.RecursionVsIterativeBenchmark::recursiveCall @ bci:17  L[0]=_ L[1]=_ L[2]=_
        # com.henryp.test.recursion.RecursionVsIterativeBenchmark::recursiveCall @ bci:17  L[0]=_ L[1]=_ L[2]=_
        # com.henryp.test.recursion.RecursionVsIterativeBenchmark::recursiveCall @ bci:17  L[0]=_ L[1]=_ L[2]=_
        # OopMap{off=104}
068
068   B5: # N94 <- 0.99998="" b3="" b4="" b6="" b7="" font="" nbsp="" req:="">
068   addq rsp, 16 # Destroy frame
popq rbp
testl rax, [rip + #offset_to_poll_page] # Safepoint: poll for GC

073   ret
073
074   B6: # B5 <- 0.00100237="" b1="" font="" nbsp="" req:="">
074   movl    RAX, RDX # spill
076   jmp,s   B5
076
078   B7: # B5 <- 0.00100137="" b2="" font="" nbsp="" req:="">
078   movl    RAX, R8 # spill
07b   jmp,s   B5
07b
07d   B8: # N94 <- 9.96996e-06="" b4="" font="" nbsp="" req:="">
07d   # exception oop is in rax; no code emitted
07d   movq    RSI, RAX # spill
080   addq rsp, 16 # Destroy frame
popq rbp

085   jmp     rethrow_stub
085

What does all this mean?

Well, I am not an assembler guru but it seems to me that this code is being partially rolled into a more iterative style

Let's go through it. Ints count and countDown are initially stored in registers rdx and rcx respectively. We know this from:


#r016 rdx   : parm 1: int
#r010 rcx   : parm 2: int


B1

(Note the stack bang - that is, preparing the stack - at B1 every time we enter this method. That can cause overhead.)


Registers "%rsp and %rbp typically hold the stack pointer and base pointer, as their names imply." [1]. So these lines push the old base pointer on the stack and then the stack pointer points 16 memory addresses lower (stacks progress "towards lower memory addresses" [2]), reserving that memory for us.

020    # stack bang

pushq   rbp
subq    rsp, #16 # Create frame


Next we test to see if our second argument (countDown or RCX) is 0

02c    testl   RCX, RCX

and if so, we jump out of the method by jumping to B6 (which then jumps to B5 that removes the stack from and leaves this code).

02e    jle,s   B6  P=0.001002 C=198529.000000

B2

Assuming countDown wasn't 0, we continue. This is the more common path as Freq is almost 1.0 (that is, a certainty).


030   B2: # B7 B3 <- b1="" b="" nbsp="">Freq: 0.998998

030    movl    R11, RCX # spill
033    decl    R11 # int


Here we put countDown into R11 (remember, RCX was our countDown value) and decrement this temporary store.

Next, we put our first argument, count, into a temporary store, R8. We increment this and XOR it with its old value.


036    movl    R8, RDX # spill
039    incl    R8 # int
03c    xorl    R8, RDX # int


And then we go back to countDown into R11 and check it's not 0, leaving the method if it is.


03f    testl   R11, R11
042    jle,s   B7  P=0.001002 C=198529.000000


If it is, we've just benefited from a recursion optimization.

B3

But it generally continues. Inside the same block of code, we're going to decrease countDown by 2 and do the same thing again:


044   B3: # B5 B4 <- 0.997996="" b2="" font="" nbsp="" req:="">
044    movl    R11, RCX # spill
047    addl    R11, #-2 # int


Exactly the same adding of 1 and XORing of count is done again but this time time with temporary storage in register RAX.


04b    movl    RAX, R8 # spill
04e    incl    RAX # int
050    xorl    RAX, R8 # int


And we again check countDown has not reached 0, ultimately dropping out of the routine if it has.

053    testl   R11, R11
056    jle,s   B5  P=0.001002 C=198529.000000

B4

I won't go into the details, but the same thing happens again. The original countDown is reduced by 3 this time and count is incremented and XORed with itself.

But this time, we do recurse with the values.

Finally

The rest of the paths end up at B5 through one path or another. (Note we poll for a garbage collection safepoint just before we leave the method. I spoke more about this here.)

Conclusion

Hotspot is making an attempt to partially tail optimize the code by making recursive code more iterative. Indeed, if the recursion was originally 2 deep, there would have been no recursion at all in the optimized code.

For all other recursions greater than 2, there is still a saving as there would be a recursion only every third calculation of count.


[1] Introduction to x64 Assembly, New York University

[2] Hacking Jon Erickson, p19.

Is Functional Faster in Java?

I've been playing with functional programming paradigms in Java and have noticed the code seems to be slower. Being curious, I thought I'd benchmark it.

To do this, I'll be using the TotallyLazy Java library to make functional programming easier and the Caliper library to do my benchmarking and make pretty pictures.

Caveat: These examples are contrived but then I'd be interested in seeing examples that were not. And my apologies to the functional community if the functional code I wrote is bad.

First, the normal 'imperative' Java code.

Here, we sum up all the numbers to a maximum:

    private final ToRun sum = new ToRun() {

        @Override

        public long run() {

            int total = 0;

            for (int i = 0; i <= SUM_OVER; i++) {

                total += i;

            }

            return total;

        }

    };

And here, we add up all the numbers in an array, adding 1 each step:

    private final ToRun mapReduce = new ToRun() {

        @Override

        public long run() {

            long total = 0;

            for (int i = 0; i < BIG_ARRAY.length; i++) {

                total += BIG_ARRAY[i] + 1;

            }

            return total;

        }

    };

The equivalent functional code looks like this for summing up to a number:

    private final Sequence      rangeSequence   = Numbers.range(0, SUM_OVER);

    private final ToRun range = new ToRun() {
        public long run() {
            Number reduce = rangeSequence. reduce(sum);
            return reduce.intValue();
        }
    };

    private final Callable2 sum = new Callable2() {

        public Number call(Number a, Number b) throws Exception {

            return a.intValue() + b.intValue();

        }

    };

And this for summing and adding 1 over an array :

    private final Sequence        bigSequence     = Sequences.sequence(BIG_ARRAY);


    private final ToRun mapReduce = new ToRun() {
        public long run() {
            Sequence map = bigSequence.map(add1Callable);
            Number reduce = map.reduce(sum);
            return reduce.longValue();
        }
    };



    private final Callable1 add1Callable = new Callable1() {
        @Override
        public Long call(Long input) throws Exception {
            return input == null ? 0 : input.longValue() + 1;
        }
    };

The ToRun class looks like this plus some code to stop our loop being optimized away :

public class Runner {

public static interface ToRun {
long run();
}

public int run(int reps, ToRun toRun) {
int doNotOptimizeAway = 0;
for (int i = 0 ; i < reps ; i++) {
doNotOptimizeAway |= (toRun.run() + i);
}
return doNotOptimizeAway;
}
}


Caliper gives results that look like this:

Where the old-fashioned Imperative way is quicker by one to two orders of magnitude.


Autoboxing

This shouldn't be too surprising as the functional library makes liberal use of autoboxing. This is very slow.

"Changing the declaration of sum from Long to long reduces the runtime from 43 seconds to 6.8 seconds on my machine. The lesson is clear: prefer primitives to boxed primitives, and watch out for unintentional autoboxing." - Joshua Bloch, Effective Java, p23.

"The programmer ignored the distinction between primitives and boxed primitives and suffered the consequences ... severe performance problems." - ibid p223

"With Sun's current compiler, measurements show that this version [lots of autoboxing] is about 60% slower than the original" - Java Generics and Collections, Maurice Naftalin, Philip Wadler.

Even the creator of the functional language, Martin Odersky says:


"If you have tight loops over arrays of primitive values, nothing beats an imperative loop."
-StackOverflow



Multithreading to the rescue?

Naively, you might think that multi-threading would help us. After all, the ability to easily parallelize code is often one of its selling points.

[Note: what I am about to do can equally be a bad idea in the imperative world.]

Multi-threading our workload is easy in TotallyLazy and looks like this:

    private final ToRun mapReduceConcurrently = new ToRun() {

        public long run() {

            Sequence map = bigSequence.mapConcurrently(add1Callable, executor);

            Number reduce = map.reduce(sum);

            return reduce.longValue();

        }

    };

    

    //

    // Threads

    //

    private ThreadFactory threadFactory = new ThreadFactory() {

        final AtomicInteger threadId = new AtomicInteger();

        @Override

        public Thread newThread(Runnable target) {

            Thread thread = new Thread(target, "PH: thread "

                    + threadId.addAndGet(1));

            thread.setDaemon(true);

            return thread;

        }

    };

    private final ExecutorService executor = Executors.newFixedThreadPool(16,

            threadFactory);

But to no avail! The results look like this:

A billion times slower = wow!

The htop command shows the CPU usage looks like this during the multi-threaded test:

When a quiescent machine looks like this:

And here is the problem:

"When parallelizing... it is generally impractical to assign a separate thread to each element ... this would require too many threads, and the overhead of coordinating them would dwarf the computation. Instead,it makes sense to partition the problem into a number of subparts, let each thread solve a subpart, and then merge the results" - Java Concurrency in Practice, Goetz et al, p101.

I emphasise again that this mistake can be made in the imperative world. I am just saying that somebody new to functional programmer might naively use the ability to easily parallelize their code and shoot themselves in the foot.

Functional Programming Crib Sheet #1 (the basics)

I've been learning functional programming over the last few months, mostly in Java and mostly with the TotallyLazy library (other libraries do exist).

It's quite a paradigm shift. To help me cope, I've compiled a crib sheet.


Reduce

"The reduceLeft method applies the passed function to the first two elements ... then applies it to the result of the first application and next element... and so on, all the way through the list." [1]

Reduce right "applies binary operation op between successive elements returned by non-empty iterator it, going right to left".

A reduce requires at least one element in the collection it works with as a reduce on a collection with one element trivially maps x to x.

TotallyLazy example


import static com.googlecode.totallylazy.Sequences.sequence;
import com.googlecode.totallylazy.Callable2;
.
.
        Callable2 reduceFn
            = new Callable2() {

            public Integer call(Integer a, Integer b) throws Exception {
                return a + b;
            }
  
        };
.
.
        sequence(1, 2, 3).reduce(reduceFn);


Produces a single integer, 6.


Folds

"A fold left operation ... involves three objects: a start value z, a list xs, and a binary operation op. The result of the fold is op applied between successive elements of the list prefixed by z." [1]

So, a fold left would look like:

op(op(op(z, a), b, c)

Or graphically:

Fold right produces right leaning trees. For instance:

op(a, op(b, op(c, z)))

or graphically:

The value z is sometimes called the seed.

Maths example

When a function is associative, you won't really see the difference between left and right folds. For instance:

(((4 + 3) + 2) + 1) = 10 = (4 + (3 + (2 + 1)))

because addition is associative.

Subtract is not, however. Therefore:

(((4 - 3) - 2) - 1) = -2 != (4 - (3 - (2 - 1))) = 2

Scala example

The Scala example is similar to the above maths but remember the seed. This will change the result but the method is the same:

    val ints: List[Int]            = List(4,3,2,1)
    def subtract(x : Int, y : Int) = { x-y }
    println(ints.foldRight(0)(subtract)) // 2   = (4 - (3 - (2 - (1 - 0)))
    println(ints.foldLeft(0)(subtract))  // -10 = ((((0 - 4) - 3) - 2) - 1)

Although fold and reduce are conceptually similar, reduce will error on an empty List.

    val abc = List("A", "B", "C")
    def myConcat(x : String, y : String) = {x + y}

    println(abc.foldRight(" the end")(myConcat)) // "ABC the end"
    println(abc.foldLeft("start: ")(myConcat))   // "start: ABC"
    println(Nil.foldRight("the end")(myConcat))  // "the end"
    println(Nil.foldLeft("the start")(myConcat)) // "the start"

    println(abc.reduceRight(myConcat))   // "ABC"
    println(abc.reduceLeft(myConcat))    // "ABC"
//    println(Nil.reduceRight(myConcat)) // blows up: Exception in thread "main" java.lang.UnsupportedOperationException: Nil.reduceRight
//    println(Nil.reduceLeft(myConcat))  // blows up too

TotallyLazy example

import static com.googlecode.totallylazy.Sequences.sequence;

import com.googlecode.totallylazy.Callable2;

.

.

        Callable2 add 

            = new Callable2() {

            public Integer call(Integer a, Integer b) throws Exception {

                return a+b;

            }

        };

.

.

        sequence(1, 2, 3).fold(1, add);

Produces a single integer: 7


Zip

Zip is NOT a cartesian product.

"The two arrays this.contents and that.contents are transformed into an array of pairs (as Tuples2s are called) using the zip operator. The zip method picks corresponding elements in its two arguments and forma an array of pairs. ...

"If one of the two operand arrays is longer than the other, zip will drop the remaining elements." [1]

TotallyLazy example

import static com.googlecode.totallylazy.Sequences.sequence;

.

.

    sequence(1, 2, 3, 4).zip(sequence(4, 5, 6))

Produces Pairs that look like:

[1,4],[2,5],[3,6]

Map

"Map[f, expr] - return the list that results from executing the function f on each element of an expr" [4].

TotallyLazy example

import static com.googlecode.totallylazy.Sequences.sequence;

import com.googlecode.totallylazy.Callable1;

.

.

        Callable1 add3 = new Callable1() {

            public Object call(Integer input) throws Exception {

                return input + 3;

            }

        };

.

.

        sequence(1, 2, 3, 4).map(add3)

Produces a Sequence that looks like:

4,5,6,7

Flat Map

This is a map then a flatten, that is it applies a function to a list and then flattens the results.

"The flatMap operator is similar to map, but it takes a function returning a list of elements as its right operand. It applies the function to each list element and returns the concatenation of all function results." [1]

"In mathematics, flat functions are called associative." [4]

TotallyLazy example

import static com.googlecode.totallylazy.Sequences.sequence;

import com.googlecode.totallylazy.Callable1;

.

.

        Callable1, ? extends Iterable

            = new Callable1, Iterable

            public Iterable

                    throws Exception {

                return input.map(add3);

            }

        };

.

.

        sequence(sequence(1, 2, 3), sequence(4, 5)).flatMap(add3Flatten);

Note how this produces a collection of collections that looks like:

{ {1, 2, 3}, {4, 5} }

Produces a Sequence like:

4,5,6,7,8

Partial function application


"Partial function application says "if you fix the first arguments of the function, you get a function of the remaining arguments" " [5] This means you can add one parameter now to the function and another later.

TotallyLazy example 


import com.googlecode.totallylazy.Function2;
.
.

    public Function2 sum() {

        return new Function2() {

            public Integer call(Integer a, Integer b) throws Exception {

                return a+b;

            }

        };

    }

.

.

Then, evaluation the sum of two numbers, 1 and 2 is trivial:

        sum().apply(1,2);

But if we wanted to add them partially:

        final Function1 onePlus = sum().apply(1);

Now it's part evaluated. At some later date, we might want to complete it, thus:

        onePlus.apply(2);

Which returns the integer 3.

Incidentally, the oder can be flipped with:

        sum().flip().apply(1);

Although this would make no difference in the case of addition.

Memoization

"In computing, memoization is an optimization technique used primarily to speed up computer programs by having function calls avoid repeating the calculation of results for previously processed inputs." [2]

The example Wikipedia gives is that of factorial:

x! = x * (x-1) * (x-2) *...

If you've calculated 5! (5*4*3*2*1 = 120) then 6! is just this times 6 (because 6! = 6 * 5 * 4 ... = 6 * 5!).


Higher Order Functions

A "higher-order function (also functional form, functional or functor) is a function that does at least one of the following:

• take one or more functions as an input
• output a function" [2]

An example familiar in mathematics is the differentiator operator. Take the function:

f(x) = x^3

and the higher order differentiation operator

d
-
dx

then this operator takes a function and returns a function:

d(f(x))
------    = 3(x^2)
  dx

In summary, it takes a function and returns a function.


[1] Programming in Scala, Odersky.
[2] Wikipedia.
[3] Wikipedia.
[4] Sal Mangano's "Mathematica Cookbook" p26.
[5] Wikipedia.